Home > Knowledge >

วงรี

Posted By Plookpedia | 10 ก.ค. 60

3,087 Views

Favorite

วงรี (ellipse)

เป็นเส้นโค้งซึ่งมีลักษณะใกล้เคียงกับวงกลมแต่มีจุดคงที่ 2 จุด เรียกว่า จุดโฟกัสของวงรี เส้นโค้งนี้เกิดจากการเคลื่อนที่ของจุด ซึ่งมีผลบวกของระยะจากจุดเคลื่อนที่ไปยังจุดโฟกัส (focus) ทั้งสองมีค่าคงที่เสมอ การเขียนวงรีกระทำได้ง่ายมาก โดยใช้เข็มหมุดปักไว้สองที่เอาเส้นด้ายมีความยาวพอสมควร ผูกปลายทั้งสองไว้กับเข็มหมุดทั้งสอง ใช้ปลายดินสอดึงเส้นด้ายให้ตึงอยู่ตลอดเวลา แล้วเคลื่อนปลายดินสอไปบนแผ่นกระดาษ ก็จะได้เส้นโค้งรูปวงรีโดยรอบ จะสังเกตได้ว่าเมื่อจุดโฟกัสทั้งสองอยู่ใกล้กัน รูปวงรีก็จะมีลักษณะใกล้รูปวงกลมมากขึ้น และ เมื่อจุดโฟกัสทั้งสองซ้อนกันก็จะได้รูปวงกลมทันที

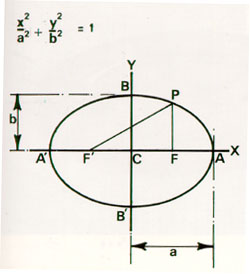
เมื่อลากเส้นตรงให้ผ่านจุดโฟกัส F และ F'ทั้งสองไปตัดวงรีที่ A และ A' ความยาวของ AA' ให้เท่ากับ 2a เราเรียก AA' ว่า แกนยาวของวงรี และ จะเห็นได้ว่า PF+PF' = 2a เสมอ แบ่งครึ่ง AA' ที่ C แล้วลากเส้นตั้งฉากกับ AA' ที่ C ไปตัดวงรีที่ B และ B' เราเรียกว่า BB' ว่า แกนสั้นของวงรี และ ให้ความยาวของ BB' เท่ากับ 2b เราเรียกจุด C ว่า จุดศูนย์กลางของวงรี ถ้าใช้แกนยาวเป็นแกนราบ และ แกนสั้นเป็นแกนดิ่งโดยมีจุดศูนย์กลางเป็นจุดกำเนิด จะได้สมการของรูปวงรีเป็นแบบ

x^2/a^2 + y^2/b^2 = 1

ในทางดาราศาสตร์พบว่า ทางเดินของโลก และ ดาวเคราะห์ต่างๆ ที่เดินรอบดวงอาทิตย์ต่างก็ล้วนมีเส้นทางเป็นรูปวงรี โดยมีดวงอาทิตย์อยู่ที่จุดโฟกัสของวงรีแต่ละวง ดวงจันทร์ซึ่งเป็นดาวบริวารของดาวเคราะห์ก็เดินทางรอบดาวเคราะห์เป็นวงรี แม้ดาวเทียมที่มนุษย์ประดิษฐ์ขึ้น ก็หมุนรอบโลกเป็นวงรี นักวิทยาศาสตร์ยังได้พบว่า แม้แต่ในปรมาณูของธาตุต่างๆ เช่น อิเล็กตรอนก็เดินทางเป็นวงรีรอบนิวเคลียสของปรมาณูนั้นๆ

เราอาจนำเส้นโค้งแบบวงรีไปออกแบบเป็นเครื่องใช้ก็ได้ เช่น จานเปล ถังเปล เป็นต้น เราจะสังเกตว่ารถบรรทุกน้ำมันมักจะมีตัวถังเป็นรูปทรงกระบอก ซึ่งมีหน้าตัดเป็นรูปวงรี สนามกีฬาที่มีลู่แข่งขันกันก็มีลักษณะเกือบเป็นวงรี

เว็บไซต์ทรูปลูกปัญญาดอทคอมเป็นเพียงผู้ให้บริการพื้นที่เผยแพร่ความรู้เพื่อประโยชน์ของสังคม ข้อความและรูปภาพที่ปรากฏในบทความเป็นการเผยแพร่โดยผู้ใช้งาน หากพบเห็นข้อความและรูปภาพที่ไม่เหมาะสมหรือละเมิดลิขสิทธิ์ กรุณาแจ้งผู้ดูแลระบบเพื่อดำเนินการต่อไป